Capitolo 3: Operazioni sui numeri binari nel microprocessore
3.1 Introduzione
In un computer, le operazioni aritmetiche vengono eseguite in 8 bit, 16 bit, 32 bit o 64 bit. Un numero come 3 in binario è 11. Se l'operazione deve essere fatta a 8 bit, questo viene considerato come 00000011; precedendolo con 0 zeri.
Per un numero binario come 10000101, il bit più significativo è quello all'estrema sinistra. È 1 in questo caso. Il bit meno significativo è il bit estremo a destra, che è ancora 1, per il numero. Il bit più significativo è abbreviato come MSB. Il bit meno significativo è abbreviato in LSB.
La cifra binaria è abbreviata in BIT e viene scritta semplicemente come bit. Nel numero 10010011 ogni uno o zero è un bit. Un gruppo di quattro bit è chiamato nibble. Un gruppo di otto bit è chiamato byte. Un byte è composto da due nibble. Il nibble inferiore è il nibble per LSB e il nibble superiore è il nibble per MSB.
Un gruppo di 8 bit, 16 bit, 32 bit o 64 bit è chiamato parola, purché tale gruppo convogli informazioni oltre la semplice indicazione di un numero. Il gruppo viene chiamato parola, ad esempio, se si tratta di un'istruzione di basso livello nel computer. Esiste anche una parola di 24 bit, ma oggi non è comunemente usata.
Endianness si riferisce all'ordine in cui i byte formano una parola. Considera la parola a 24 bit: 100100001111010100100010. Questa parola è composta da tre byte che sono:
10010000 11110101 00100010
Il byte più significativo è il byte più a sinistra. Quando il byte all'estrema sinistra è il byte più significativo e il byte all'estrema destra è il byte meno significativo, si parla di rappresentazione Big Endian della parola. La rappresentazione Little Endian è l'opposto.
La memoria del computer è una serie di celle e ciascuna cella contiene un byte. La prima cella nella memoria del computer è per il byte 0, la seconda per il byte 1, la terza per il byte 2 e così via. Con big endianness e per la parola precedente, il byte più significativo è memorizzato nella cella del byte 0, il byte centrale è memorizzato nella cella del byte 1 e il byte meno significativo è memorizzato nella cella del byte 2. Ciò significa che ci sono più byte significativi nella cella di memoria inferiore.
La parola precedente a 24 bit può essere scritta in ordine inverso di byte come segue:
00100010 11110101 10010000
Ora, il byte meno significativo è all'estrema sinistra e il byte più significativo è all'estrema destra. Quando il byte all'estrema sinistra è il byte meno significativo e il byte all'estrema destra è il byte più significativo, è la rappresentazione Little Endian della parola. Con poca endianness e per la parola precedente, il byte meno significativo è memorizzato nella cella del byte 0, il byte centrale è memorizzato nella cella del byte 1 e il byte più significativo è memorizzato nella cella del byte 2. Ciò significa che nella cella di memoria inferiore c'è un byte meno significativo.
L'endianness non viene utilizzato per i bit in un byte. Inoltre non viene utilizzato per i bocconcini in un byte. Viene utilizzato solo per l'ordine dei byte.
La linea dei numeri
Un numero senza segno è un numero positivo. I numeri positivi sono numeri che vanno dallo zero verso l'alto. Esistono anche numeri negativi. I numeri positivi e negativi possono essere presentati su una linea numerica. La seguente linea numerica mostra i numeri interi positivi e negativi (interi) vicini allo zero:
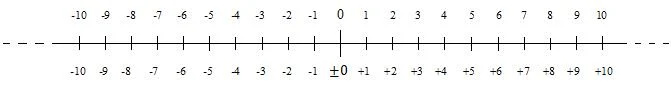
I numeri negativi diminuiscono da zero verso il basso (verso sinistra). In molte situazioni, lo zero è considerato positivo. Tuttavia, in alcune situazioni è considerato negativo. Ecco perché nel diagramma davanti allo zero nella numerazione più bassa si trovano i segni più e meno. Quando un numero è positivo, il suo segno può essere omesso; questo è il caso della numerazione superiore nel diagramma. Il segno meno davanti a un numero negativo non viene mai omesso.
3.2 Addizione di numeri binari
In aggiunta:
A + B = S
A è detto augendo, B è detto addendo e S è detta somma.
Consideriamo la seguente addizione di due numeri positivi in base due:

In base due, le uniche cifre possibili sono 0 e 1. L'addizione in base 2 è simile all'addizione in base dieci, ma due in base due è uno-zero (10). Quando la somma di due bit in una colonna è 10, viene scritto 0 e 1 viene riportato nella colonna immediatamente sinistra; da aggiungere alla somma dei due bit lì. Quando la somma totale è tre, significa 11 in base due. Viene scritto l'1 di destra su 11 e l'1 di sinistra viene aggiunto alla somma dei bit immediati della colonna di sinistra. In entrambi i casi, l'1 portato a sinistra è chiamato riporto.
Leggendo la tabella di addizione precedente da destra, nella seconda colonna (da destra), c'è un riporto che risulta da 1+1 = 10. Nella terza colonna, c'è un riporto che risulta da 1+1+ riporto di 1 = 11. Nella quarta colonna, c'è un riporto che risulta da 0+1+ riporto di 1 = 10. Nella quinta colonna, non c'è riporto perché la somma è 0+0+ riporto di 1 = 1. Il riporto il resto delle colonne non comporta alcun riporto.
Il conteggio delle colonne inizia dall'estremità destra. Con l'addizione a 16 bit, può esserci un riporto dall'ottava colonna alla nona colonna (spostandosi verso sinistra). La tabella seguente illustra ciò:

Le operazioni aritmetiche e logiche si svolgono nel microprocessore sulla scheda madre del computer.
Per un computer con parole a 8 bit, il riporto non può passare automaticamente dall'ottavo bit al nono bit tramite l'hardware. Quindi, per aggiungere due gruppi da 16 bit in un computer di questo tipo, l'addizione deve essere eseguita due volte in coppie di otto-otto bit. Il riporto viene movimentato ed effettuato dal software (programmazione).
Per sommare due numeri, i numeri possono essere convertiti prima nella forma del complemento a due (vedi sotto) prima della somma.
3.3 Complemento a due e sua sottrazione di numeri binari
Sulla scheda madre del computer c'è la memoria, il microprocessore e altri circuiti. La memoria è una serie di celle da otto bit. Per un byte, ogni bit va in una cella. Il microprocessore ha alcune posizioni di tipo memoria. Queste posizioni di tipo memoria sono chiamate registri. Quindi, nel computer, gruppi di byte possono essere immagazzinati temporaneamente nella memoria o nei registri del microprocessore.
In ognuno di questi depositi, ogni cella può contenere un 1 o uno 0 e nient'altro. Nella vita ci sono numeri positivi e numeri negativi. Un numero positivo inizia con un segno più (+) e un numero negativo inizia con un segno negativo (-). Quando il segno viene omesso, il numero viene considerato positivo.
Per risolvere il problema di indicare il segno di un numero nel computer, i numeri interi vengono memorizzati in intervalli. I numeri interi sono interi. Se vengono utilizzati otto bit per memorizzare l'intervallo di numeri possibili, il bit più a sinistra viene utilizzato come bit di segno. Se il numero inizia con 0, il numero è un numero positivo. Se inizia con 1, il numero è un numero negativo. Se vengono utilizzati sedici bit per memorizzare l'intervallo di numeri possibili, il bit più a sinistra viene utilizzato come bit di segno. Se il numero inizia con 0, t il numero è un numero positivo. Se inizia con 1, il numero è un numero negativo. I numeri in questa forma sono chiamati numeri con segno.
In pratica, possono esserci numeri con segno per 8 bit, 16 bit, 32 bit e 64 bit. Maggiore è il numero di bit utilizzati, maggiore è la gamma di possibili numeri che possono essere memorizzati.
Interi in complemento a due
Con il complemento a due, i numeri positivi sono i normali numeri di conteggio, tranne per il fatto che la cifra più a sinistra è 0. Per ottenere il numero negativo corrispondente per ogni dato numero positivo, invertire ciascun bit del numero e aggiungere 1 al risultato. L'invertito o complemento di 0 è 1. L'invertito o complemento di 1 è 0. Le seguenti tabelle mostrano alcuni numeri in complemento a due nei loro intervalli:
| Tabella 3.31 Interi in complemento a due a due bit |
|
|---|---|
| Binario | Decimale |
| 01 | +1 |
| 00 | +0 |
| undici | -1 |
| 10 | -2 |
I numeri binari positivi sono 00 e 01 (ovvero zero e uno). Nel bit più a sinistra, lo zero indica che si tratta di numeri positivi. 00 è un po' al centro dell'intervallo. Per ottenere -1, l'inverso del numero 01 risulta essere 10. Sommando 1 a questo (all'estrema destra) si ottiene 11.
Poiché vengono utilizzati due bit, ne rimane solo uno per rappresentare i numeri nell'intervallo costituito dai numeri +1, +0 e -1 corrispondenti a 01, 00 e 11. Il primo bit indica il segno. Succede che 10 per +2 non sia tra questi tre numeri binari. 10 inizia con 1, il che significa che deve essere un numero negativo in complemento a due. Quindi, 10 è incluso nell'intervallo, il che significa -2.
Con due bit in complemento a due, il numero di tutti gli interi (positivi e negativi) rappresentabili è 2 2 = 4 e non 2 2 -1 = 3. La sfumatura risulta dall'inclusione dell'ultimo numero negativo che è il negativo di 2 numerocon – 1. In questo caso, -2 2-1 = -2 1 = -2. Non c'è +2 nell'intervallo dei numeri in complemento a due in 2 bit.
| Tabella 3.32 Interi in complemento a due a quattro bit |
|
|---|---|
| Binario | Decimale |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
I numeri binari positivi vanno da 0000 a 0111 (cioè da zero a sette). Nel bit più a sinistra, lo zero indica che si tratta di numeri positivi. 0000 è un po' a metà dell'intervallo. Per ottenere -1, l'inverso del numero 0001 risulta essere 1110. Aggiungendo 1 a questo (all'estrema destra) si ottiene 1111. Per ottenere -2, l'inverso di 0010 risulta essere 1101. Aggiungendo 1 a questo ( dall'estrema destra) dà 1110. Gli altri numeri binari negativi come da -3 a -7 sono determinati in modo simile.
Poiché vengono utilizzati quattro bit, rimangono tre bit per rappresentare i numeri nell'intervallo che sono +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 e -7 corrispondenti a 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 e 1001.
Il -8 che corrisponde a 1000 deve essere indirizzato separatamente. Il primo bit di tutti questi numeri indica il segno 0 per i numeri positivi e 1 per i numeri negativi. Succede che 1000 non sia tra questi quattordici numeri binari. 1000 inizia con 1, il che significa che deve essere un numero negativo, per quanto riguarda il complemento a due. Pertanto, 1000 è incluso nell'intervallo, il che significa -8.
Con quattro bit in complemento a due, il numero di tutti gli interi (positivi e negativi) rappresentabili è 2 4 = 16 e non 2 4 – 1 = 15. La sfumatura risulta dall'inclusione dell'ultimo numero negativo che è il negativo di 2 numeroLarghezza – 1. In questo caso, -2 4 -1 = -2 3 = -8. Non c'è +8 nell'intervallo di numeri.
L'analisi precedente per due, quattro e bit più ampi in complemento a due può essere applicata a numeri binari di larghezza 8 bit, 16 bit, 32 bit e 64 bit.
Il complemento a due sacrifica il primo bit (più a sinistra) per il segno 0 per il numero positivo e 1 per il numero negativo. Per il gruppo di bit ampio “n”, ce ne sono 2 N totale dei numeri positivi più negativi. Sarebbero 2 N -1, se non fosse per l'ultimo fortunato numero negativo (il più piccolo) incluso. Il numero positivo più alto è +2 n-1 -1 e il numero negativo più piccolo è -2 n-1 -1. Sarebbe -2 n-1 -1, se non fosse stato per il fortunato -2 n-1 incluso.
Sottrazione di numeri in complemento a due
In sottrazione:
A-B = D
A si chiama minuendo, B si chiama sottraendo e D si chiama differenza.
Per sottrarre un numero binario positivo da un altro numero binario positivo, il minuendo viene scritto in complemento a due e il sottraendo viene convertito nel suo valore in complemento a due negativo. Quindi, l'affermazione matematica diventa:
A+ – B = D
In altre parole, nella sottrazione in complemento a due, il sottraendo viene convertito in un numero negativo e quindi aggiunto al minuendo.
Esempio 3.31:
Valuta la seguente espressione decimale in complemento a due utilizzando quattro bit:
6 – 4
Soluzione:
Il numero binario per 6 è 110. Nel complemento a due a 4 bit, è 0110. Il numero binario per +4 è 100. Nel complemento a due a 4 bit, è 0100. 0100 che deve essere convertito in meno 4 in due complementare come segue: Il complemento o l'inversione di 0100 è 1011. Aggiungendo 1 a questo dall'estremità destra, come abbiamo fatto in aggiunta, si ottiene 1100. Quindi, l'espressione decimale è:
6 – 4 che diventa:
0110 – 0100 che è
0110 +(– 0100) = 0110 + 1100 fatto come nella sezione di addizione precedente come:

Nota: 0110 +(– 0100) è uguale a 6 + – 4
Con la sottrazione del complemento a due, qualsiasi riporto, dopo l’ultima colonna a sinistra, nell’addizione, viene scartato. Quando si sottrae in formato decimale, l'affermazione matematica è:
6 – 4 = 2
Facendo la stessa cosa in complemento a due, la risposta è 0010 che è +2 nel conteggio binario in complemento a due. La sottrazione precedente sottrae un numero più piccolo da un numero più grande. Nell'esempio seguente, un numero più grande viene sottratto da un numero più piccolo. È possibile consultare la tabella 3.32 per vedere se 0010 è veramente il complemento a due che equivale a +2.
Esempio 3.32:
Valuta la seguente espressione decimale in complemento a due con quattro bit:
4 – 6
Soluzione:
Il numero binario per 4 è 100. Nel complemento a due a 4 bit, è 0100. Il numero binario per +6 è 110. Nel complemento a due a 4 bit, è 0110. 0110 deve essere convertito in 6 negativo nel complemento a due come segue: Il complemento o l'inversione di 0110 è 1001. Aggiungendo 1 a questo dall'estremità destra, come abbiamo fatto nell'addizione precedente, si ottiene 1010. Quindi, l'espressione decimale è:
4 – 6 che diventa:
0100 – 0110 che è
0100 +(– 0110) = 0100 + 1010 fatto come nella sezione di addizione precedente come:

Nota: 4+ – 6 equivale a 0100 +(– 0110).
Con la sottrazione del complemento a due, qualsiasi riporto, dopo l’ultima colonna a sinistra, nell’addizione, viene scartato. Quando si sottrae in formato decimale, l'affermazione matematica è:
4 – 6 = -2
Facendo la stessa cosa in complemento a due, la risposta è 1110 che è -2 nel conteggio binario in complemento a due. È possibile consultare la tabella 3.32 per vedere se 1110 è veramente il complemento a due che equivale a -2.
3.4 Moltiplicazione di numeri binari
Nella dichiarazione:
A x B = P
A è detto moltiplicando, B è detto moltiplicatore e P è detto prodotto. L'espressione A x B significa aggiungere A, B numero di volte quando A e B sono numeri interi (numeri interi).
La moltiplicazione in binario è uguale alla moltiplicazione in decimale. Tuttavia, invece di farlo in decimale, viene fatto in binario. La moltiplicazione dell'espressione decimale di 42 x 10 viene eseguita in binario come segue dove 42 10 = 101010 2 e 10 10 = 1010 2 :
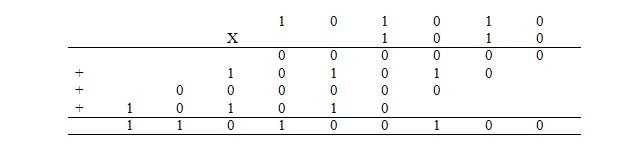
I 4 numeri aggiunti vengono definiti prodotti parziali. La risposta è il prodotto. L'aggiunta dei prodotti parziali avviene nello stesso modo spiegato in precedenza.
La moltiplicazione può anche essere vista come segue: In questa moltiplicazione in base due, se il bit (cifra) nel moltiplicatore è 1, il bit meno significativo del suo prodotto parziale è il bit meno significativo del moltiplicando che viene riscritto direttamente sotto di esso; e il resto dei bit del moltiplicando si ripetono verso sinistra. In questa moltiplicazione in base due, se il bit (cifra) nel moltiplicatore è 0, il suo prodotto parziale è costituito da 0 con il bit meno significativo di 0 direttamente sotto di esso. Il numero di tutti zeri è il numero di bit nel moltiplicando.
3.5 Divisione dei numeri binari
Nella dichiarazione:
A ÷ B = Q
A si chiama Dividendo, B si chiama Divisore e P si chiama Quoziente. Il quoziente può essere accompagnato da un resto. L'espressione A ÷ B indica quante volte B può essere aggiunto per dare A o avvicinarsi ad esso in modo tale che il resto sia 0 o inferiore a B.
La divisione può essere effettuata in molti modi. La divisione mostrata qui è la divisione di restauro.
Divisione Restauro
Questo è il metodo della divisione lunga che si impara a scuola. Se 237 viene diviso per 6, la risposta è 39 resto 3. Il 237 10 in base 2 è 11101101 2 e 6 10 in base 2 è 110 2 . Il 39 10 in base 2 è 100111 2 e 3 10 in base 2 è 11 2 .
Quindi, 11101101 2 diviso per 110 2 dà 100111 2 resto 11 2 in base due. Con il metodo di ripristino, i numeri binari sono numeri ordinari e non sono necessariamente in complemento a due. La seguente struttura divide 11101101 2 entro 110 2 dare 100111 2 resto 11 2 :

La sottrazione viene eseguita normalmente e non utilizzando il complemento a due. Poiché questa è la base due, un prestito è due e non dieci. I dividendi parziali sono 10, 101, 1011, 1010 e 1001. 11 è il resto. Poiché il divisore ha tre cifre, la divisione viene effettuata fondamentalmente in gruppi di tre cifre del dividendo indicato. Il quoziente è il numero intero (intero) e per questo problema è 100111. Il risultato del quoziente e del resto è quello previsto.
3.6 Operazioni aritmetiche con software e hardware
La scheda madre del computer ha un orologio. I ticchettii dell'orologio si chiamano impulsi. Ad ogni impulso di clock vengono prese una o più decisioni in punti diversi della scheda madre; e questo ha a che fare con la programmazione (software).
All'interno del microprocessore sono presenti due tipi di circuiti chiamati: circuiti logici combinatori e circuiti logici sequenziali. Esiste un altro tipo di circuito chiamato multiplexer. L'addizione, la moltiplicazione e la divisione possono avvenire entro un intervallo di orologio utilizzando la logica combinatoria (circuito). Durante la programmazione (software) la decisione viene presa ad ogni impulso di clock utilizzando circuiti logici sequenziali e multiplexer.
Quando la sottrazione viene eseguita utilizzando il complemento a due, sono necessari almeno due impulsi di clock. Al primo impulso di clock, un multiplexer incanala il sottraendo a una serie di porte NOT (una porta NOT per cifra). Al secondo impulso di clock, la logica combinatoria aggiunge 1 all'uscita delle porte NOT e continua ad aggiungere il sottraendo e il minuendo risultanti. Tutta questa aggiunta può avvenire entro un intervallo di orologio.
L'addizione, la moltiplicazione e la divisione possono ancora essere eseguite con la programmazione utilizzando le tabelle della verità. Tuttavia, non è trattato in questo corso di carriera online.
3.7 Operazioni logiche nel microprocessore
AND, OR, XOR e Inverti
E
La tabella seguente illustra l'AND bit a bit. Ciò significa che per due diversi numeri binari, i bit corrispondenti vengono messi in AND in base alla tabella AND Truth:
Muovendosi da sinistra a destra, 1 AND 1 = 1; 0 E 1 = 0; 0 E 0 = 0; 1 E 0 = 0; e così via secondo la tabella della verità AND.
O
La tabella seguente illustra l'OR bit a bit. Ciò significa che per due numeri binari diversi, i bit corrispondenti vengono sottoposti a OR in base alla tabella OR Truth:

Muovendosi da sinistra a destra, 1 OR 1 = 1; 0 O 1 = 1; 0 OPPURE 0 = 0; 1 O 0 = 1; e così via secondo la tabella della verità OR.
GRATUITO
La tabella seguente illustra l'OR esclusivo bit a bit. Ciò significa che per due numeri binari diversi, i bit corrispondenti vengono sottoposti a XOR in base alla tabella di verità XOR:

Muovendosi da sinistra a destra, 1 XOR 1 = 0; 0XOR1 = 1; 0XOR0 = 0; 1XOR0 = 1; e così via secondo la tabella della verità XOR.
Inverti (NO)
La tabella seguente illustra il NOT bit a bit (inversione). Ciò significa che per un numero binario, questa volta, ogni bit viene invertito in base alla tabella di verità NOT:

Muovendosi da sinistra a destra, NON 1 = 0; NON 0 = 1; NON 0 = 1; NON 1 = 0; e così via secondo la Tabella della Verità NOT.
Spostamento a destra o a sinistra
Sposta a destra
Il seguente numero binario viene spostato di 3 posizioni di bit a destra, con gli zeri inseriti nelle posizioni di bit libere a sinistra:

Lo spostamento può essere effettuato per uno, due, tre, quattro, ecc.
Sposta a sinistra
Il seguente numero binario viene spostato di 3 posizioni di bit a sinistra, con gli zeri inseriti nelle posizioni di bit libere a destra:

Lo spostamento può essere effettuato per uno, due, tre, quattro, ecc.
Rotazione a destra o a sinistra
La rotazione è simile allo spostamento. Si fa un po' alla volta. Quando si ruota verso destra, le punte che lasciano l'estremità destra non cadono come nello spostamento; sostituiscono i bit lasciati liberi a sinistra, uno per uno. Quando si ruota a sinistra, le punte che lasciano l'estremità sinistra non cadono come nello spostamento; sostituiscono i bit lasciati liberi sulla destra, uno per uno.
Ruota a destra
Il seguente numero binario viene ruotato di 3 posizioni di bit a destra:

La rotazione può essere fatta per uno, due, tre, quattro, ecc. posti.
Ruota a sinistra
Il seguente numero binario viene ruotato di 3 posizioni di bit a sinistra:

La rotazione può essere fatta per uno, due, tre, quattro, ecc. posti.
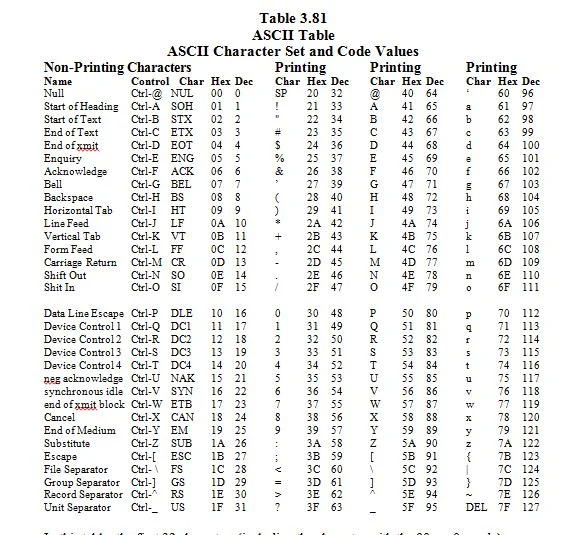
3.8 Set di caratteri ASCII e relativi valori del codice
ASCII sta per “American (U.S.A) Standard Code for Information Interchange”. Immagina una tastiera con 96 tasti. Questa è una tastiera ideale in cui i tasti delle lettere maiuscole sono diversi dai tasti delle lettere minuscole. Ogni altro tasto rappresenta un carattere che si trova su una tastiera inglese (USA). I caratteri e i codici (numeri corrispondenti ai caratteri) sono elencati di seguito:
In questa tabella, i primi 32 caratteri (incluso il carattere con 00 16 = 0 10 codice) sono caratteri non stampabili. Sono personaggi di controllo. Non si vedono sullo schermo (monitor) dove tutto è uguale. Hanno solo effetti. Ne parleremo più avanti.
Il resto dei caratteri sono caratteri stampati; vengono visualizzati sullo schermo. Sono presenti 128 caratteri ASCII. 2 7 = 128.1.111.111 2 = 127 10 . Il 7 in 2 7 significa 7 bit.
Ora, 1111111 2 +1 2 equivale a:
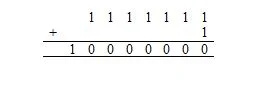
Qui, 10.000.000 2 = 128 10 . Sono 128 10 caratteri nell'elenco (tabella) precedente di caratteri ASCII. Ciò include il carattere null, il cui codice in base sedici (esadecimale) è 00, che equivale a 0 in base dieci.
Poiché ci sono 128 caratteri in totale, 128 meno 32 caratteri non stampabili danno come risultato 96 caratteri stampabili. In questa sezione si presuppone che esista una tastiera ideale con 96 caratteri stampabili. Su questa tastiera ideale, i tasti per i caratteri inglesi maiuscoli sono diversi dai tasti per i caratteri inglesi minuscoli.
Ogni carattere sulla tastiera è rappresentato da un numero in base due di 7 bit che non sono mostrati nell'elenco. La lettera maiuscola di “N”, ad esempio, è rappresentata dai sette bit 1001110 in base 2. Per convertire 1001110 2 in base 16, precederlo con 0 e raggruppare il risultato in sottogruppi di quattro bit come segue:
| 0100| 1110| 2 = | 4| E| 16
Questo è 01001110 2 = 4E 16 . Per convertire 4E 16 alla base dieci, procedere come segue:
4x(16) 1 + E x (16) 0 = 4x16 + Ex1 = 4x16 + 14x1 = 64 + 14 = 78 10
A destra di 'N' nell'elenco (tabella) c'è il numero esadecimale di 4E e il numero decimale di 78.
Come altro esempio, il carattere “[“ è rappresentato dai sette bit 1011011 in base 2. Per convertire 1011011 2 in base 16, precederlo con 0 e raggruppare il risultato in sottogruppi di quattro bit come segue:
| 0101| 1011| 2 = | 5| B | 16
Questo è 01011011 2 = 5B 16 . Per convertire 5B16 in base dieci, procedere come segue:
5x(16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
A destra di '[' nell'elenco (tabella) c'è il numero esadecimale di 5B e il numero decimale di 91.
Ancora un altro esempio, il carattere per il numero decimale “5” è rappresentato dai sette bit 0110101 in base 2 e non 0000101 in base 2. Per convertire 0110101 2 in base 16, precederlo con 0 e raggruppare il risultato in sottogruppi di quattro bit come segue:
| 0011| 0101| 2 = | 5| B | 16
Questo è 00110101 2 = 35 16 . Per convertire 3516 in base dieci, procedere come segue:
3x(16) 1 + 5 x (16) 0 = 3x16 + 5x1 = 3x16 + 5x1 = 48 + 5 = 53 10
A destra del “5” nell’elenco (tabella) c’è il numero esadecimale 35 e il numero decimale 53.
Poiché il computer funziona a byte, quando viene premuto un tasto sulla tastiera ideale, vengono inviati otto bit al microprocessore (scheda madre). La tastiera ideale è una periferica separata dall'unità di sistema (base) del computer. Ha un circuito elettronico (IC) che crea i sette bit e lo precede con uno zero prima di inviarlo attraverso il suo cavo alla scheda madre dell'unità di sistema. Dalla porta di ingresso (circuito di ingresso) della scheda madre va al microprocessore anch'esso presente sulla scheda madre. Dal microprocessore si passa alla memoria, anch'essa alloggiata sulla scheda madre.
Pertanto, quando viene premuto il tasto “N” sulla tastiera ideale, otto bit 01001110 vengono trasferiti al microprocessore. Dal microprocessore vengono portati nella memoria dove rimangono in una posizione di memoria come byte. Il programmatore di computer dovrebbe tenere presente che gli otto bit di 01001110 2 è uguale a 4E 16 che è uguale a 78 10 .
Quando viene premuto il tasto “[“sulla tastiera ideale, otto bit 01011011 vengono trasferiti al microprocessore. Dal microprocessore vengono portati nella memoria dove rimangono in una posizione di memoria come byte. Il programmatore di computer dovrebbe tenere presente che gli otto bit di 01011011 2 è uguale a 5B 16 che è uguale a 91 10 .
Quando viene premuto il tasto “5” della tastiera ideale, come carattere e non come numero decimale, vengono portati al microprocessore otto bit 00110101. Dal microprocessore vengono portati nella memoria dove rimangono in una posizione di memoria come byte. Il programmatore di computer dovrebbe tenere presente che gli otto bit di 00110101 2 è uguale a 35 16 che è uguale a 5310 10 .
Ci sono momenti in cui un programma è in esecuzione e attende che il numero decimale 5 venga inserito nel computer. In questa situazione, se viene premuto il tasto “5” sulla tastiera ideale, il codice a otto bit 00110101 viene comunque trasferito al microprocessore. Poiché ciò che serve è il numero decimale 5, e non il carattere '5', un pezzo di codice (programma breve) dalla memoria utilizza il microprocessore per convertire il codice carattere 00110101 in base due nel numero in complemento a due 00000101 2 prima di inviarlo a una posizione di memoria come byte in complemento a due. Il programmatore di computer deve tenere presente che 00000101 significa 5 10 in base 2, ed è diverso dai numeri di codice di 00110101 2 , 35 16 e 53 10 che significa il carattere di '5'. Per visualizzare in memoria il numero in complemento a due di 00000101, un altro breve programma deve convertire 00000101 dalla memoria in 00110101. È 00110101 che è uguale a 35 16 che è uguale a 53 10 visualizzato sul monitor (o stampato su carta dalla stampante).
3.9 Formato numero in virgola mobile
Un numero senza parte decimale è un numero intero. Il numero 36 è un numero intero. 36.375 non è un numero intero. È un numero decimale con una parte decimale. La parte decimale di .375 è una frazione inferiore a 1.
36.375 viene interpretato in forma decimale come:
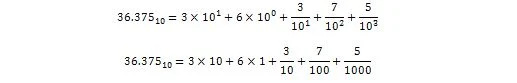
Ora:
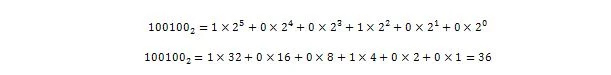
Quindi, 100100 2 = 3610 che è la parte intera di 36.375 10 .
Ora:
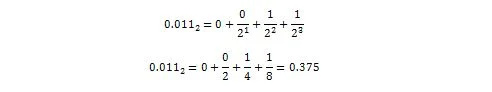
Quindi, 0,011 2 = 0,375 10 che è la parte decimale di 36.375 10 .
∴ 36.375 10 = 100100.011 2
Mettiamola in un altro modo:
100100.011 2 = 36.375 10
I numeri sono rappresentati nel computer in base 2 e non in base 10, a parità di tutto. Poiché una cella in un registro del microprocessore o una cella in memoria può contenere solo 1 o 0, non c'è spazio per memorizzare un punto decimale. Ciò pone un problema. Come risoluzione, esiste la rappresentazione in virgola mobile a 32 bit a precisione singola IEEE-754 e la rappresentazione in virgola mobile a 64 bit a doppia precisione IEEE-754.
Formato numero in virgola mobile a 32 bit
Il numero 100100.0112 può essere espresso come:
100100.011 2 = 1.00100011 2 x2 +5
Il lato destro del simbolo = è indicato in matematica come la forma standard in base due del lato sinistro di 100100.011 2 .
Ora, 00100011 di 1.00100011 2 a destra del simbolo =, senza il prefisso “1”. e senza il 2 come base, è chiamato significando esplicito. In questo caso, il punto binario viene preso cinque posti a sinistra in modo da avere “1”. Non confondere tra punto decimale e punto binario. Il punto binario è per la base 2, mentre il punto decimale è per la base 10. L'“1”. seguito da 00100011 a destra del simbolo =, senza il 2 come base, forma il vero significando. Tuttavia, 1.00100011 è chiamato significando implicito.
Dopo il significato sul lato destro c'è 'x 2 +5 ' espressione. Con questa espressione il +5 si chiama esponente. Il segno più significa che il punto binario deve essere spostato di cinque posti in avanti per trovarsi nella sua normale posizione originale e 2 è la base per la numerazione. L’equazione precedente può essere scritta al contrario come:
1.00100011 2 x2 +5 = 100100.011 2
Con la rappresentazione in virgola mobile a 32 bit, è “1.00100011 2 x2 +5 ' che viene utilizzato e non solo '100100.011 2 ”. Il 2 per la base non viene registrato. La rappresentazione in virgola mobile a 32 bit per “1.00100011 2 x2 +5 ” numero, che è pari a 36.375 10 = 100100.011 2 , è riportato nella tabella seguente:

Esistono posizioni a 32 bit numerate dall'estremità destra, a partire da 0. Il primo bit all'estremità sinistra è il bit di segno. Se il numero è positivo, questo bit è 0. Se il numero è negativo, questo bit è 1 (-1 è composto da due caratteri e non può essere inserito in nessuna cella). Il 1.00100011 2 x2 +5 che è pari a 36.375 10 che è anche uguale a 100100.011 2 è un numero positivo. Quindi il primo bit è 0.
Ci sono otto posizioni di bit per l'esponente, a partire dalla posizione 30 fino alla posizione 23 inclusa. Tuttavia, l'esponente scritto lì è 10000100 2 che è uguale a 132 10 . L'esponente del numero di interesse è in realtà +5 della base di due. Allora, cosa succede?
Ora, nel formato a 32 bit, un esponente pari a 0 viene scritto come 01111111 2 che è uguale a 127 10 . Il +5 10 è +101 2 . Quindi, arrivando a 10000100 2 nella parte dell'esponente nella tabella, 101 2 è stato aggiunto a 01111111 2 , corrispondentemente. Significa che 5 è stato aggiunto a 127 per avere 132 10 .
Il significando, senza “1.”, ha portato le posizioni da 22 a 15 incluse. Tieni presente che 1 di '1'. non è stato indicato nella stringa a 32 bit. Non è mai indicato: accettalo. Il resto delle celle fino alla posizione 0 sono riempite con zeri.
Se l'esponente effettivo è -5, allora 5 viene sottratto da 127 10 averne 122 10 . Ciò corrisponde a sottrarre 101 2 dallo 01111111 2 avere 01111010 2 .
Con tutta l'illustrazione precedente, il numero +1 che è uguale a 1,0 x 2 0 = 1,0 x 1 = 1,0 è rappresentato come:

Si noti che il valore '1'. di 1,0 x 2 0 non è indicato nel formato. Non è mai indicato. La successiva frazione mista che va positivamente dopo 1.0 è:

Notare l'1 all'estremità destra. Questa rappresentazione è il numero:

La differenza tra 1.0000001192092896 e 1.0 è:
1.0000001192092896 – 1.0 = 0.0000001192092896
I numeri con parti decimali sono frazioni miste. Non tutte le frazioni comprese tra 1 10 e 2 10 possono essere rappresentati nel computer. Si può presumere che il divario frazionario più piccolo tra i numeri misti consecutivi con il formato in virgola mobile a 32 bit sia 0,0000001192092896. Si prevede che l'intervallo per la doppia precisione sia più piccolo. Fare riferimento alla seguente illustrazione.
Rappresentando il numero, 0.0 non segue gli argomenti precedenti. La rappresentazione per 0.0 è dichiarata e deve essere appresa come tale. Per rappresentare 0,0, tutte le celle per il significando sono 0 e anche tutte le celle per l'esponente sono zero. Il bit di segno può essere 0 o 1. Sfortunatamente, ciò dà origine a 0 positivo e 0 negativo come segue:

Nella vita reale esiste solo uno zero. Lo 0 positivo e lo 0 negativo non esistono. Tuttavia, 0 è generalmente considerato positivo. Lo 0 positivo e lo 0 negativo esistono qui a causa di questa particolare descrizione del formato. La linea numerica (vedi sopra) può anche avere +0 e -0, ma esiste solo uno zero.
Formato numero in virgola mobile a 64 bit
Il formato a virgola mobile a 64 bit è simile al formato a 32 bit, ma con le seguenti differenze:
- Ci sono 64 bit per rappresentare un numero.
- Dopo il bit del segno ci sono 11 bit per il numero dell'esponente.
- Il numero dell'esponente per l'indice zero (2 0 ) è 1023 10 =01111111111 2 .
- Gli undici bit sono seguiti da 52 bit per il significato esplicito.
- Ha una gamma di numeri più ampia rispetto al formato a 32 bit.
Si noti che il valore '1'. cioè all'inizio del significato non è ancora compreso tra i 64 bit, così come non è compreso tra i 32 bit per il formato a 32 bit.
Una delle differenze più importanti tra il formato a 64 bit e il formato a 32 bit è che la differenza tra le frazioni miste consecutive nel formato a 64 bit è inferiore a quella del formato a 32 bit.
Nel formato a 64 bit, l'intervallo (gap) tra 1.0 e la frazione mista successiva può essere calcolato come segue:
1.0 è
0 01111111111 00000000000000000000 00000000000 000000000000000000000 2
Ciò equivale a “1.”, che non è stato indicato nella stringa, moltiplicato per 2 elevato alla potenza (indice) 0 (con esponente pari a 1023 10 =01111111111 2 per 2 0 = 1). La stringa è 1,0 x 2 0 .
La successiva frazione mista maggiore di 1,0 è:
0 01111111111 00000000000000000000 00000000000 000000000000000000001 2
Ciò equivale a “1”. che non è indicato nella stringa, seguito da 51 zeri, e poi 1, moltiplicato per 2 elevato a 0 (con esponente 1023 10 =011111111112 2 per 2 0 = 1). Questo è lo stesso di:
+2 0 ×(1+2− -52 ) ≈ 1.0000000000000002
Il ≈ significa approssimativamente uguale a.
Ora:
1.0000000000000002 – 1.0 ≈ 0.0000000000000002
Il valore dell'intervallo corrispondente per un formato a 32 bit è 0,0000001192092896 ≈ 0,00000012.
0.0000000000000002 è molto più piccolo di 0.00000012. Pertanto, ci sono molte più frazioni miste tra due numeri interi consecutivi (ad esempio 3 e 4) nel formato a 64 bit che tra due numeri interi consecutivi nel formato a 32 bit.
Il numero di frazioni miste tra due numeri interi consecutivi sulla linea numerica è infinito. Pertanto, nessun formato (ad esempio 32 bit o 64 bit) può fornire tutte le frazioni miste tra due numeri interi consecutivi (numeri interi). Minore è il divario (intervallo) tra due numeri interi consecutivi fornito da un formato (ad esempio 32 bit o 64 bit), maggiore è il numero di frazioni miste tra i numeri interi consecutivi (per la linea numerica).
Il motivo per cui il formato a 64 bit è descritto come precisione doppia o superiore, rispetto al formato a 32 bit, è che l'intervallo tra due frazioni miste consecutive delimitate da due numeri interi consecutivi per il formato a 64 bit è inferiore al corrispondente 32 intervallo di formato a -bit. Inoltre, ci sono più possibili frazioni miste tra due numeri interi limitati per il formato a 64 bit rispetto a quelle corrispondenti per il formato a 32 bit.
Conversione di una parte decimale (frazione) di un numero decimale in una parte binaria
Il 36.375 è un numero decimale con la parte decimale “.375”. La parte decimale di “.375” è una frazione compresa tra zero e uno. Lo 0,5 in base dieci ha lo stesso valore di 1/2 in base due. Lo 0,5 10 che si esprime con lo sviluppo in base due è:
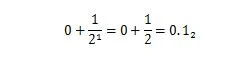
Non è 0,101 2 che significa 0,625 10 . La parte decimale di un numero decimale ha la sua parte binaria equivalente per il numero binario corrispondente. Quindi, per convertire un numero decimale come 36.375 10 in base due, converti 36 in binario e poi converti anche .375 in binario. Quindi, unisci entrambi i risultati con il punto binario. I metodi per convertire le due sezioni sono diversi. Come convertire un intero decimale in base 2 è spiegato nel capitolo 1.
Per convertire la frazione decimale in frazione binaria, attenersi alla seguente procedura:
- Moltiplicare la frazione decimale (parte decimale) per 2. Il numero intero che ne risulta è la prima cifra binaria.
- Ripeti il passaggio precedente con il risultato decimale frazionario per ottenere la cifra binaria successiva.
- Continua a ripetere il passaggio precedente finché il risultato frazionario decimale non sarà .0000—.
Esempio: converti la parte frazionaria di 36.375 10 alla parte frazionaria equivalente in base due.
Soluzione:
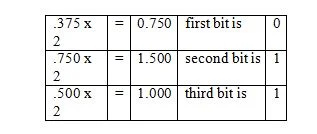
Si noti che nel terzo passaggio è stato moltiplicato .500 per 2 e non 1.500. La frazione binaria corrispondente viene letta nell'ultima colonna dall'alto. E quindi, il seguente risultato è:
.375 10 = 0,011 2
Conversione di una parte binaria (frazione) di un numero binario in una parte decimale
Per ottenere ciò, espandi la frazione binaria in potenze reciproche di 2.
Esempio: convertire la parte frazionaria di 100100.011 2 alla parte frazionaria equivalente in base dieci.
Soluzione:
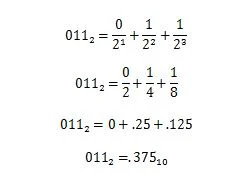
3.10 Prefissi numerici nell'informatica
Nella vita normale, 1 chilo significa 1000 che si abbrevia in k (minuscolo) come in 1 kg. In informatica, 1 chilo significa 2 10 = 1024, ma è abbreviato in K (maiuscolo) come in 1Kbit. Nella vita normale, 1 mega significa 1.000.000 che è abbreviato in M (maiuscolo) come in 1Mg. In informatica, 1 mega significa 2 venti = 1.048.576 = 2 10 x2 10 = 1024 x 1024 = 1.048.576 ed è ancora abbreviato in M (maiuscolo) come in 1Mbits. Nella vita normale, 1 giga significa 1.000.000.000 è abbreviato in G (maiuscolo) come in 1Gg. In informatica, 1 giga significa 2 30 = 1.073.741.824 = 2 10 x2 10 x2 10 = 1024 x 1024 x 1024 = 1.073.741.824 ed è ancora abbreviato in G (maiuscolo) come in 1Gbit. La tabella seguente fornisce il significato di quattro prefissi nella vita normale e nell'informatica:
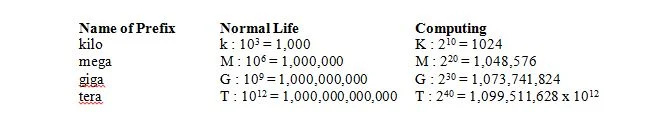
3.11 Problemi
Si consiglia al lettore di risolvere tutti i problemi in un capitolo prima di passare al capitolo successivo.
- Disegna una linea numerica con numeri interi da -10 a +10.
- Aggiungi i seguenti numeri binari in complemento a due a 8 bit: 101010 2 e 1111 2 .
- Utilizzare solo l'approccio del complemento a due a 8 bit per sottrarre il numero binario di 1111 2 dal numero binario di 101010 2 .
- Trova il prodotto di 10110 2 x1101 2 in base due.
- Dividere 36.375 10 entro il 1000 10 in decimale e in binario e confrontare i risultati.
- Utilizza gli 8 bit di tua scelta per illustrare l'AND logico, OR, XOR, Inverti, Sposta a destra, Sposta a sinistra, Ruota a destra e Ruota a sinistra. Ogni byte dovrebbe avere un misto di 1 e 0.
- a) Scrivere il codice numerico per il carattere ASCII zero in esadecimale, binario e decimale.
b) Scrivere il codice numerico per il carattere ASCII “1” in esadecimale, binario e decimale.
c) Scrivere il codice numerico per il carattere ASCII di “A” in esadecimale, binario e decimale.
d) Scrivere il codice numerico per il carattere ASCII di “a” in esadecimale, binario e decimale. - Converti 49,49 10 in base due. Converti il risultato nel formato a virgola mobile IEEE a 32 bit.
- a) In cosa differisce il formato a virgola mobile IEEE a 64 bit dal formato a 32 bit?
b) Fornire le due ragioni correlate per cui il formato a 64 bit è descritto come una precisione doppia o superiore rispetto a
Formato a 32 bit.