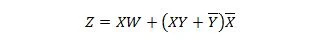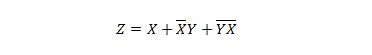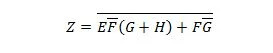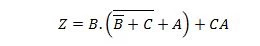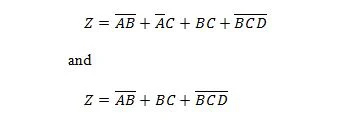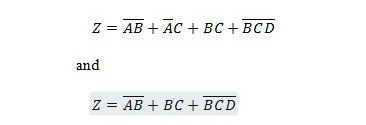Capitolo 2: Algebra booleana e relativi componenti informatici

Capitolo 2: Algebra booleana e relativi componenti informatici

2.1 Operatori booleani di base

Supponiamo che io (l'autore) sia alto e tu (il lettore) sei alto. Se qualcuno ti chiedesse se siamo entrambi alti, diresti 'Sì' (vero). Se ti chiede se siamo entrambi bassi, diresti 'No' (falso). Se tu sei basso e io sono alto, e lui ti chiede se tu o io siamo alti, la tua risposta sarebbe 'Sì' (vero). Se ti chiedesse se sia io che te siamo alti, non avresti una risposta. Potresti proseguire dicendo che l'ultima domanda non dovrebbe essere posta o che la domanda non ha una risposta. Ebbene, voglio che tu (il lettore) sappia che oggi, in determinate circostanze, la domanda dovrebbe essere posta.

In biologia, una persona è alta o bassa. Sono le condizioni “ambientali” che fanno sì che la persona abbia una statura media. Uno scienziato, George Boole, ha definito una serie di risposte o regole per questo tipo di domande. Impareremo queste regole in questa sezione del corso di carriera online (capitolo). Queste regole sono oggi utilizzate nell'informatica, nella programmazione, nell'elettronica e nelle telecomunicazioni. Senza queste regole, infatti, non avreste il computer, come è comune oggi; non avresti nemmeno la programmazione, come è comune oggi.

Vero o falso
Una semplice affermazione del linguaggio umano è vera o falsa in sé. Se dico “sono alto” questo può essere vero o falso. Se dico “sei alto” o è vero o è falso. Se io sono alto e tu sei basso, e viene posta la domanda se sia tu che io siamo alti, nella logica booleana, deve essere data una risposta vero o falso. Quale dei due dovrebbe essere dato? Boole non ha realmente risposto a questa domanda. Ha semplicemente inventato una serie di regole da seguire. La buona notizia è che, quando si seguono queste regole nel loro giusto contesto, non si creano ambiguità. Grazie a queste regole, oggi abbiamo i computer e la programmazione. Le regole ti sono state date adesso. Le regole non possono davvero essere spiegate; li accetti e basta. Le regole sono suddivise in tre voci: AND, OR e NOT.

E
La domanda può essere posta se sia tu che io siamo alti. La mia altezza e la tua altezza vengono quindi combinate dall'insieme di regole AND. Queste sono le regole AND da seguire:

falso E falso = falso
falso E vero = falso
vero E falso = falso
vero E vero = vero

Ora, lasciamo che alto sia vero e breve sia falso. Ciò significa che se io sono basso E tu sei basso, tu ed io siamo bassi. Se io sono basso E tu sei alto, tu ed io siamo bassi; questa è la risposta booleana che devi accettare. Se io sono alto E tu sei basso, sia tu che io siamo bassi. Se io sono alto E tu sei alto, tu ed io siamo alti. Tutte queste sono regole booleane AND che tu (il lettore) devi semplicemente accettare.

O
La domanda può essere posta se tu o me siamo alti. La mia altezza e la tua altezza vengono quindi combinate dalle regole OR. Queste sono le regole della sala operatoria da seguire:

falso O falso = falso
falso O vero = vero
vero O falso = vero
vero O vero = vero

Ancora una volta, lascia che alto sia vero e breve sia falso. Ciò significa che se io sono basso O tu sei basso, tu O io siamo bassi. Se io sono basso O tu sei alto, tu o io siamo alti. Se io sono alto O tu sei basso, tu O io siamo alti. Se io sono alto O tu sei alto, tu o io siamo alti. Tutte queste sono regole booleane che devi accettare.

NON
Ora, nella logica booleana, esistono solo due stati (risposte possibili). Cioè, se NON sei alto, sei basso. Se NON sei basso, sei alto; nient'altro. Queste sono le regole NON da seguire:

NON falso = vero
NON vero = falso

Supponiamo di avere una corda (o una molla) che puoi estendere (tirare). Mentre la corda è nel suo stato naturale, se dico 'NON corta', la allungheresti; questa è l'interpretazione. Mentre la corda è estesa, se dico 'NON lunga', le consentiresti di contrarsi; questa è l'interpretazione.

Devi memorizzare tutte le regole indicate nelle loro diverse categorie.

Più di due operandi
In un linguaggio informatico, AND, OR e NOT sono chiamati operatori. Per l'operatore NOT, è necessario un solo operando (valore per un operatore) per avere una risposta. Per gli operatori AND o OR è possibile avere più di due operandi. I casi precedenti mostrano due operandi per AND e OR. È possibile avere tre operandi per AND come segue:

falso E falso E falso = falso
falso E falso E vero = falso

Queste sono due linee; ciascuno ha due operatori AND. In realtà ci sono nove righe quando gli operandi sono tre. Con l'operatore AND, solo l'ultima riga (nona riga) è uguale a true; tutte le righe precedenti sono false. Si noti che con due operandi AND, solo l'ultima riga è ancora vera; tutte le tre righe precedenti sono false. Quando gli operandi sono quattro, ci sono 16 righe e solo l'ultima riga è vera per l'operatore AND.

Il modello per AND e il modello per OR sono diversi. Con tre operandi per due operatori OR, ci sono anche nove righe e solo la prima riga, questa volta, è falsa. La riga dalla seconda alla nona è vera. Si noti che con due operandi per OR, solo la prima riga è ancora vera; tutte le restanti tre righe sono false. Quando gli operandi sono quattro per OR, ci sono anche 16 righe.

L'operatore NOT tratta un solo operando. Il NON falso è vero e il NON vero è falso.

2.2 Tabella della verità a due operandi e loro componenti elettronici

In matematica esiste un argomento chiamato algebra. Una piccola parte di essa è stata vista nel capitolo precedente. Esiste un tipo di algebra chiamata algebra booleana. Nell'algebra booleana, il vero è identificato dalla cifra in base due che è 1 e il falso è identificato dalla cifra in base due che è 0.

I componenti interni dell'unità computer sono componenti elettronici. L'unità di sistema del sistema informatico dispone di componenti elettronici digitali. L'operazione AND viene eseguita da un piccolo componente elettronico chiamato porta AND. L'operazione OR viene eseguita dal piccolo componente elettronico chiamato porta OR. L'operazione NOT viene eseguita dal piccolo componente elettronico chiamato porta NOT. Troppe di queste porte possono trovarsi in un chip di circuito integrato (IC).

AND Tavola della Verità e la sua Porta
La tabella seguente fornisce la tabella della verità AND e il simbolo della porta AND (piccolo circuito):

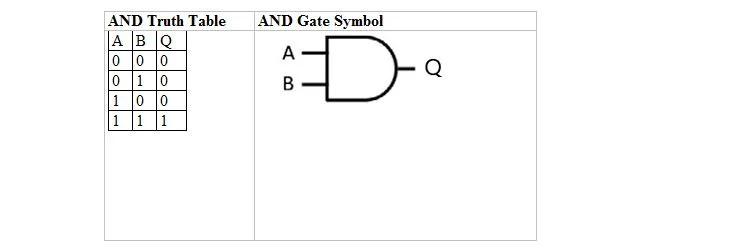
Sia per la tabella di verità AND che per la sua porta, A e B sono due variabili di input. Q è la variabile di uscita. A è 1 o 0. B è 1 o 0. Q è 1 o 0. La tabella di verità AND con 1 e 0 è la stessa della precedente disposizione (tabella) di verità AND vero/falso. L'equazione AND è:

UN . B = Q

dove il punto (.) significa AND (Booleano). Il punto può essere omesso per avere AB = Q che significa la stessa cosa (AND).

Nota: i bit per A e B nelle quattro righe, a coppie, sono i primi quattro numeri in base due a partire da 0 (o 00), cioè 00, 01, 10, 11.

La tabella seguente fornisce la tabella della verità OR e il simbolo della porta OR (piccolo circuito):

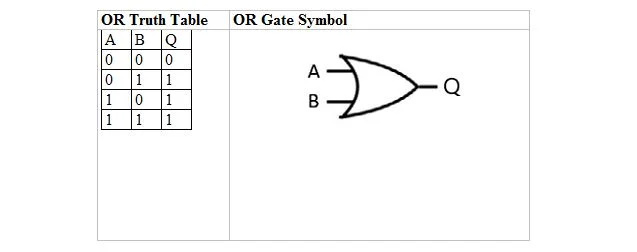
Sia per la tabella di verità OR che per la sua porta, A e B sono due variabili di input. Q è la variabile di uscita. La tabella di verità OR con 1 e 0 è la stessa della precedente disposizione (tabella) di verità OR vero/falso.

L'equazione OR è:

A + B = Q

Dove il + qui significa OR booleano e non addizione. L'equazione viene letta come 'A o B uguale Q'.

La tabella seguente fornisce la tabella della verità NOT e il simbolo della porta NOT (piccolo circuito):

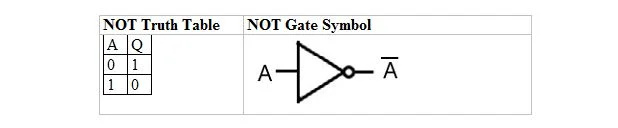
La tabella di verità NOT o porta NOT ha solo un ingresso e un'uscita. Quando l'ingresso è 0, l'uscita è 1. Quando l'ingresso è 1, l'uscita è 0. La porta NOT esegue una sorta di inversione. La variabile di output è uguale alla variabile di input, ma con una barra (sopralineata). La tabella di verità NOT con 1 e 0 è la stessa della precedente disposizione (tabella) di verità vero/falso OR.

L'equazione NOT è:

A = Q

Dove Q = A e la barra sopra A qui significa complemento. Il complemento di 0 è 1 e il complemento di 1 è 0. La porta NOT è anche conosciuta come porta INVERTENTE.

Queste sono le tavole di verità fondamentali (o radice) e le loro porte (piccoli circuiti) nell'elettronica digitale (con l'algebra booleana). Le altre tre tavole di verità fornite nell'illustrazione seguente e i relativi cancelli sono per comodità e si basano sulle tre tavole di verità precedenti.

Sono presenti una tabella di verità e una porta che derivano dalla tabella e dalla porta di verità AND. Sono chiamate tabella della verità NAND (per NOT AND) e la corrispondente porta NAND. La tabella della verità NAND e la sua porta NAND sono:

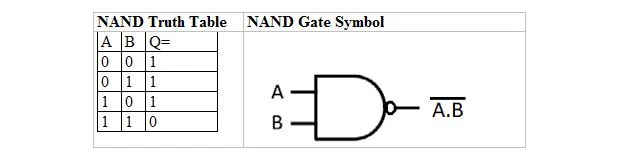
Per ottenere la tabella di verità NAND, vai all'output della tabella di verità AND e sostituisci ogni cifra con il suo complemento. Il complemento di 0 è 1 e il complemento di 1 è 0. La porta NAND è come la porta AND, ma ha un piccolo cerchio prima della linea di uscita. L'equazione NAND è:

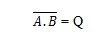
Dove significa il complemento del risultato di “A” E “B”. La barra (sopra la linea) è rappresentata nel cancello dal cerchietto. Nota che il punto tra A e B può essere omesso.

C'è un'altra tabella di verità e un cancello che derivano dalla tabella di verità e dal cancello OR. Sono chiamate tavola di verità NOR (per NOT OR) e la corrispondente porta NOR. La tavola di verità NOR e la sua porta NOR sono:

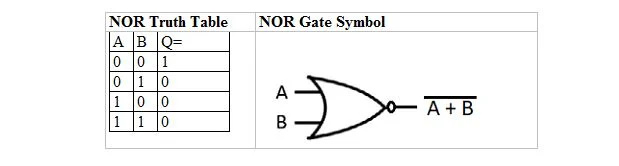
Per ottenere la tabella di verità NOR, vai all'output della tabella di verità OR e sostituisci ogni cifra con il suo complemento. Il complemento di 0 è 1 e il complemento di 1 è 0. La porta NOR è come la porta OR, ma ha un piccolo cerchio prima della linea di uscita. L'equazione NOR è:

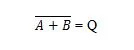
Dove 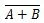indica il complemento del risultato di “A” O “B”. La barra (sopra la linea) è rappresentata nel cancello dal cerchietto.

OR esclusivo (XOR)
La tabella della verità per la porta OR è:

Nell'inglese normale, non è chiaro se l'ultima riga di 1 OR 1 debba dare 1 o 0. Quindi, nell'algebra booleana, ci sono due tipi di tabelle di verità OR e due porte corrispondenti. Con l'OR normale, l'ultima riga di 1 OR 1 dà 1. L'altro tipo di OR è l'OR esclusivo (XOR) dove le prime tre righe sono uguali alle prime tre righe dell'OR normale (incluso l'output). Tuttavia, per la quarta e ultima riga, 1 OR 1 dà 0.

La tabella seguente fornisce la tabella della verità XOR e il simbolo della porta XOR (piccolo circuito):

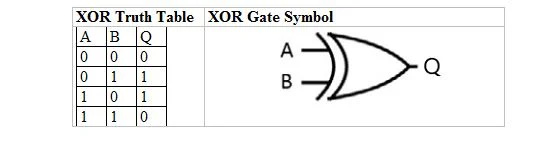
Sia per la tabella di verità XOR che per il suo gate, “A” e “B” sono due variabili di input. “Q” è la variabile di uscita.

L'equazione XOR è:

A ⊕ B = Q

Dove ⊕ qui significa XOR booleano.

Il normale OR significa uno o entrambi. OR esclusivo significa rigorosamente O e non entrambi.

2.3 Postulati booleani

I postulati sono ipotesi in base alle quali si traggono determinate conclusioni. Esistono dieci postulati booleani che derivano dalle equazioni AND, OR e NOT (tabelle della verità). Queste equazioni sono anche chiamate funzioni. Le funzioni fondamentali sono così ricopiate:

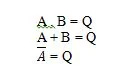
Queste sono le funzioni fondamentali (equazioni) nell'algebra booleana. Le seguenti altre tre equazioni (di funzioni) non sono funzioni fondamentali:

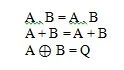
Sebbene l'ultima funzione qui sia peculiare, non è considerata una funzione fondamentale.

I postulati booleani sono i seguenti:

Dalla funzione AND
1) 0 . 0 = 0
venti . 1 = 0
3)1. 0 = 0
4)1. 1 = 1

Dalla funzione OR
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1

Dalla funzione NOT
9) 0 = 1
10) 1 = 0

Nota: Questi postulati sono semplicemente le linee nelle tabelle di verità AND, OR e NOT espresse in modo indipendente. Il lettore dovrebbe memorizzare i postulati indicati.

2.4 Proprietà booleane

Una proprietà è come una caratteristica di qualcosa. Le proprietà booleane sono equazioni derivate dai postulati booleani. In questa sezione, le proprietà vengono semplicemente fornite senza le loro derivazioni e poi utilizzate successivamente. Ci sono venticinque proprietà raggruppate in dieci intestazioni come segue:

Proprietà della funzione AND

Proprietà 1:

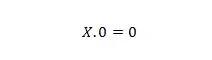
Dove X può essere 1 o 0. Ciò significa che, qualunque sia X, il risultato è sempre 0.

Nota: una variabile non deve necessariamente essere A o B o C o D. Una variabile può essere W o X o Y o Z o qualsiasi altra lettera.

Proprietà 2:

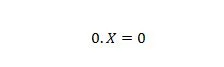
Dove X può essere 1 o 0. Nota che la differenza tra la proprietà 1 e la proprietà 2 è che sul lato sinistro del segno uguale di entrambe le equazioni, le posizioni di X e 0 sono scambiate.

Proprietà 3:

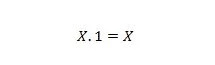
Se X è 0, allora 0. 1 = 0. Se X è 1, allora 1. 1 = 1.

Proprietà 4:

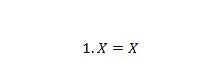
Se X è 0, allora 1. 0 = 0. Se X è 1, allora 1. 1 = 1. Nota che la differenza tra la proprietà 3 e la proprietà 4 è che sul lato sinistro di entrambe le equazioni, le posizioni di X e 1 vengono scambiati.

Proprietà della funzione OR

Proprietà 5:

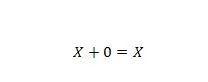
Dove X può essere 1 o 0. Ciò significa che se X è 0, il risultato è 0. Se X è 1, il risultato è 1.

Proprietà 6:

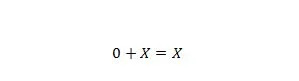
Dove X può essere 1 o 0. Nota che la differenza tra la proprietà 5 e la proprietà 6 è che sul lato sinistro di entrambe le equazioni, le posizioni di X e 0 sono scambiate.

Proprietà 7:

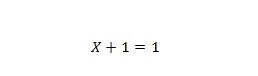
Se X è 0, allora 0 + 1 = 1. Se X è 1, allora 1 + 1 = 1.

Proprietà 8:

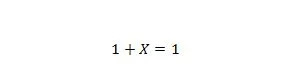
Se X è 0, allora 1 + 0 = 1. Se X è 1, allora 1 + 1 = 1. Nota che la differenza tra la proprietà 7 e la proprietà 8 è che sul lato sinistro di entrambe le equazioni, le posizioni di X e 1 vengono scambiati.

Proprietà riguardanti la combinazione di una variabile con se stessa o con il suo complemento

Proprietà 9:

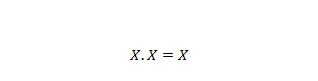
Cioè: se X è 0, allora 0 . 0 = 0. Se X è 1, allora 1 . 1 = 1.

Proprietà 10:

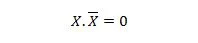
Cioè: se X è 0, allora 0. 1 = 0. Se X è 1, allora 1. 0 = 0.

Per variabili consecutive, questa proprietà diventa:

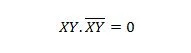
Proprietà 11:

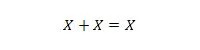
Cioè: se X è 0, allora 0 + 0 = 0. Se X è 1, allora 1 + 1 = 1 (dal normale OR).

Proprietà 12:

Cioè: se X è 0, allora 0 + 1 = 1. Se X = 1, allora 1 + 0 = 1.

Cioè: se X è 0, allora 0 + 1 = 1. Se X = 1, allora 1 + 0 = 1.

Doppia complementazione

Proprietà 13:

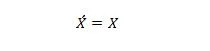
Quando X a sinistra è 0, X a destra diventa 0. Quando X a destra è 1, X a sinistra diventa 1. In altre parole, i doppi complementi restituiscono il valore originario.

Diritto commutativo

Proprietà 14:

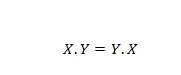
Ciò significa che lo scambio del primo e del secondo operando per l'operatore AND, a sinistra del segno uguale, non ha importanza; la risposta è sempre la stessa dopo che è avvenuto lo scambio sul lato sinistro. Questa equazione può essere scritta omettendo i punti come: XY = YX.

Proprietà 15:

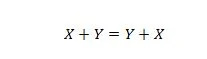
La spiegazione qui è la stessa dell'operatore AND precedente, ma è per l'operatore OR.

Diritto distributivo

Proprietà 16:

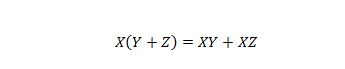
Qui ci sono tre variabili: X, Y e Z. Ciascuna variabile può essere 1 o 0. Sul lato sinistro del simbolo uguale, le parentesi significano valutare prima cosa c'è dentro. Quindi, AND è il risultato con X. Il lato destro dice che X AND Y insieme, O X AND Z insieme, sono uguali al lato sinistro. Si noti che l'operatore punto per gli AND viene omesso completamente; e le variabili unite significano ancora AND.

Proprietà 17:

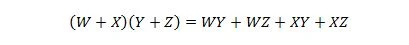
Questa proprietà è un'estensione della proprietà 16 con la variabile aggiunta di W.

Diritto associativo

Proprietà 18:

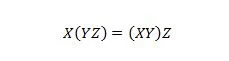
Le parentesi significano valutare prima cosa c'è tra parentesi. Quindi, per l'espressione sul lato sinistro, se Y con Z viene messo prima in AND e X viene messo in AND con il risultato, allora il risultato finale sul lato sinistro è uguale al risultato finale a destra -lato mano dove X con Y viene messo in AND prima di mettere il risultato in AND con Z. Notare che i punti sono stati omessi nell'equazione.

Proprietà 19:

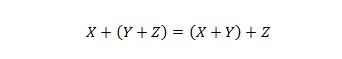
Questa proprietà è spiegata in modo simile alla proprietà 18, ma viene utilizzato l'operatore OR al posto dell'operatore AND. L'operatore OR + non viene mai omesso da un'espressione booleana per ragioni di semplicità. D'altra parte, l'operatore AND può essere omesso e le due variabili possono essere unite.

Assorbimento

Proprietà 20:

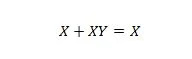
Con questa equazione, qualunque sia Y, il lato destro sarà sempre X (assorbito).

Proprietà 21:

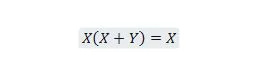
Inoltre, con questa equazione, qualunque sia Y, il lato destro sarà sempre X (assorbito). Questa proprietà 21 è la stessa della proprietà 20 che è:

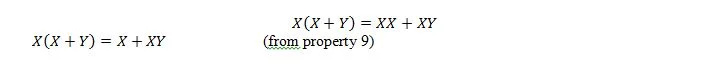
Qui usiamo la legge distributiva e il fatto che X.X = X della proprietà 9.

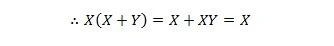
Un'identità

Proprietà 22:

Ciò significa che per l'espressione X + Y, il complemento di X davanti a Y non modifica l'espressione.

Proprietà 23:

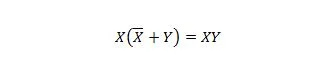
Ciò significa che per l'espressione XY, il complemento di X ORed con Y tra parentesi, che viene eseguito per primo, non modifica l'espressione XY.

Legge di DeMorgan

Proprietà 24:

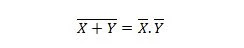
Ciò significa che una porta NOR (NOT OR) ha lo stesso risultato di NOTARE i due ingressi prima di inserirli in AND.

Proprietà 25:

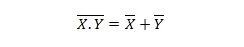
Ciò significa che una porta NAND (NOT AND) ha lo stesso risultato di NOTARE i due ingressi prima dell'OR.

Le illustrazioni fornite rappresentano le 25 proprietà. Possono essere dimostrati sostituendo tutti i diversi valori possibili di 1 e 0, in ciascuna espressione sul lato sinistro, per vedere se si ottiene l'espressione (o il risultato) sul lato destro. Le dimostrazioni sono lasciate come esercizio al lettore.

2.5 Semplificazione delle espressioni composte

Le due funzioni seguenti sono identiche:

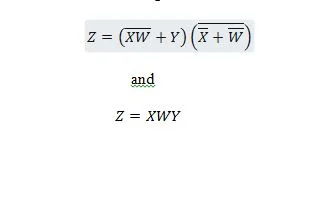
Z è l'output e X, W e Y sono gli input. Il primo necessita di una porta NAND, una porta OR, una porta AND, due porte NOT, una porta OR e una porta NOR. Il secondo necessita solo di due porte AND. La prima è un'equazione con un'espressione composta, sul lato destro, che è stata semplificata (ridotta) al singolo termine dell'espressione a destra per la seconda equazione.

La semplificazione o la riduzione portano a un minor numero di porte per implementare la stessa funzione di un circuito. Un circuito così più piccolo può far parte di un circuito integrato (IC) o essere un circuito autonomo sulla superficie della scheda madre del computer.

Quando una funzione (equazione) arriva al processo di progettazione, è necessario procedere a una semplificazione per ridurre il numero di porte e ottenere un circuito più economico. La semplificazione richiede l'impiego di una o più delle venticinque proprietà booleane precedenti.

Esempio 2.51:

Riduci l'equazione:

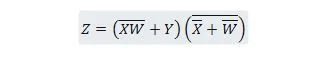
Nota: Due parentesi una accanto all'altra significano che le parentesi sono AND (il punto tra di loro facoltativamente non è stato scritto).

Soluzione:
Per le soluzioni, la giustificazione (motivo) di ciascun passaggio è riportata a destra del passaggio, tra parentesi. Il lettore dovrebbe leggere ogni passaggio e la sua giustificazione. Il lettore dovrebbe fare riferimento anche alle proprietà precedenti mentre legge i passaggi di riduzione della funzione.

Esempio 2.52:

Semplificare:

2.6 Somma Minima dei Prodotti

Le due funzioni seguenti sono identiche:

Si dice che entrambe le espressioni della mano destra di entrambe le equazioni siano nella forma Somma dei prodotti (SP). Si dice che un'espressione espressa sia nella forma Somma del prodotto se non ha parentesi. È ovvio che la prima funzione (equazione) necessita di più porte della seconda funzione.

La prima espressione della mano destra può ancora essere ridotta per ottenere la seconda funzione. La seconda espressione a destra non può essere ulteriormente semplificata ed essere comunque espressa come Somma di Prodotti (“addizione” di termini). La seconda espressione del lato destro non può essere semplificata ulteriormente. Quindi, si dice che sia nel formato della somma minima dei prodotti (MSP).

Esempio 2.61:
Portare la seguente funzione prima nel modulo Somma dei prodotti e poi nel modulo Somma minima dei prodotti.

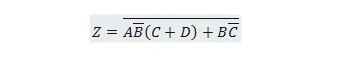
Soluzione:
Quando si risolvono problemi come questo, è necessario utilizzare una o più delle venticinque proprietà precedenti, come illustrato in questa soluzione:

2.6 Somma Minima dei Prodotti

Le due funzioni seguenti sono identiche:

Si dice che entrambe le espressioni della mano destra di entrambe le equazioni siano nella forma Somma dei prodotti (SP). Si dice che un'espressione espressa sia nella forma Somma del prodotto se non ha parentesi. È ovvio che la prima funzione (equazione) necessita di più porte della seconda funzione.

La prima espressione della mano destra può ancora essere ridotta per ottenere la seconda funzione. La seconda espressione a destra non può essere ulteriormente semplificata ed essere comunque espressa come Somma di Prodotti (“addizione” di termini). La seconda espressione del lato destro non può essere semplificata ulteriormente. Quindi, si dice che sia nel formato della somma minima dei prodotti (MSP).

Esempio 2.61:
Portare la seguente funzione prima nel modulo Somma dei prodotti e poi nel modulo Somma minima dei prodotti.

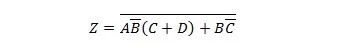
Soluzione:
Quando si risolvono problemi come questo, è necessario utilizzare una o più delle venticinque proprietà precedenti, come illustrato in questa soluzione:

Quest'ultima espressione è nel formato Somma dei prodotti (SP), ma non nel formato Somma minima dei prodotti (MSP). La prima parte della domanda ha avuto risposta. La soluzione per la seconda parte è la seguente:

Quest'ultima funzione semplificata (equazione) è in forma MSP e necessita di un numero inferiore di porte per l'implementazione rispetto alla corrispondente forma SP. Ricorda: SP significa somma dei prodotti mentre MSP significa somma minima dei prodotti.

Esempio 2.62:
Il seguente circuito ha gli ingressi X, Y e W e Z è l'uscita. Produrre la funzione Somma dei prodotti (SP) (funzione apparente della somma minima dei prodotti) per Z. Quindi, produrre la vera Somma dei prodotti (MSP) più ridotta (minimizzata). Quindi, implementa il circuito MSP (disegna la rete di gate MSP).

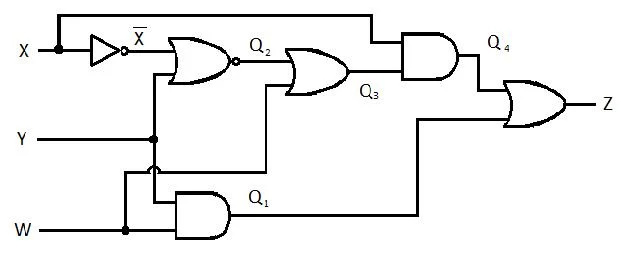
Fig 2.61 Un circuito di gate

Soluzione:
Prima che inizi il processo di semplificazione, l'espressione per Z deve essere ottenuta in termini di X, Y e W. Fare riferimento a questa illustrazione di esempio dal diagramma:

Questa è l'espressione di Z in termini di X, Y e W. Successivamente, può avvenire la semplificazione in MSP apparente. L'MSP apparente è SP.

Quest'ultima equazione (funzione) è nella forma SP. Non è vera la Somma Minima dei Prodotti (non ancora MSP). Quindi, la riduzione (minimizzazione) deve continuare.

Quest'ultima equazione (funzione) è una vera somma minima di prodotti (MSP). E il circuito di gating della somma minima dei prodotti (vera minimizzazione) è:

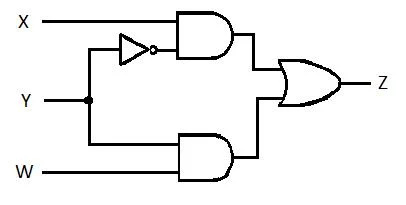
Fig 2.62 Circuito di gate MSP

Commento
Dall'analisi di questa sezione si può vedere che non è chiaro se la Somma dei Prodotti sia la Somma Minima dei Prodotti oppure no. SP non è molto utile. È MSP che è molto utile. Esiste un modo sicuro per ottenere MSP; è usare la mappa Karnaugh. Karnaugh Map va oltre lo scopo di questo corso di carriera online.

2.7 Problemi

Si consiglia al lettore di risolvere tutti i problemi in un capitolo prima di passare al capitolo successivo.

1. Produrre le tabelle di verità AND, OR e NOT con le porte corrispondenti.
2. Annota i dieci postulati booleani nelle loro diverse categorie, nominando le categorie.
3. Senza spiegazione, scrivi le ventisei proprietà dell'algebra booleana nelle loro diverse categorie, nominando le categorie.
4. Riduci l'equazione utilizzando le proprietà booleane e citando le categorie utilizzate.



5. Riduci l'equazione utilizzando le proprietà booleane e citando le categorie utilizzate.



6. Utilizzando le proprietà booleane e citando le categorie utilizzate, riduci la seguente equazione, prima alla Somma dei prodotti e poi alla Somma minima dei prodotti:



7. Utilizzando le proprietà booleane e citando le categorie utilizzate, riduci la seguente equazione, prima alla Somma dei prodotti e poi alla Somma minima dei prodotti: